In my summary of the Kaggle bulldozer price forecasting competition, I mentioned that part of my solution was based on stochastic gradient boosting. To reduce runtime, the number of boosting iterations was set by minimising the loss on the out-of-bag (OOB) samples, skipping trees where samples are in-bag. This approach was motivated by a bug in scikit-learn, where the OOB loss estimate was calculated on the in-bag samples, meaning that it always improved (and thus was useless for the purpose of setting the number of iterations).
The bug in scikit-learn was fixed by porting the solution used in R’s GBM package, where the number of iterations is estimated by minimising the improvement on the OOB samples in each boosting iteration. This approach is known to underestimate the number of required iterations, which means that it’s not very useful in practice. This underestimation may be due to the fact that the GBM method is partly estimated on in-bag samples, as the OOB samples for the Nth iteration are likely to have been in-bag in previous iterations.
I was curious about how my approach compares to the GBM method. Preliminary results on the toy dataset from scikit-learn’s documentation looked promising:
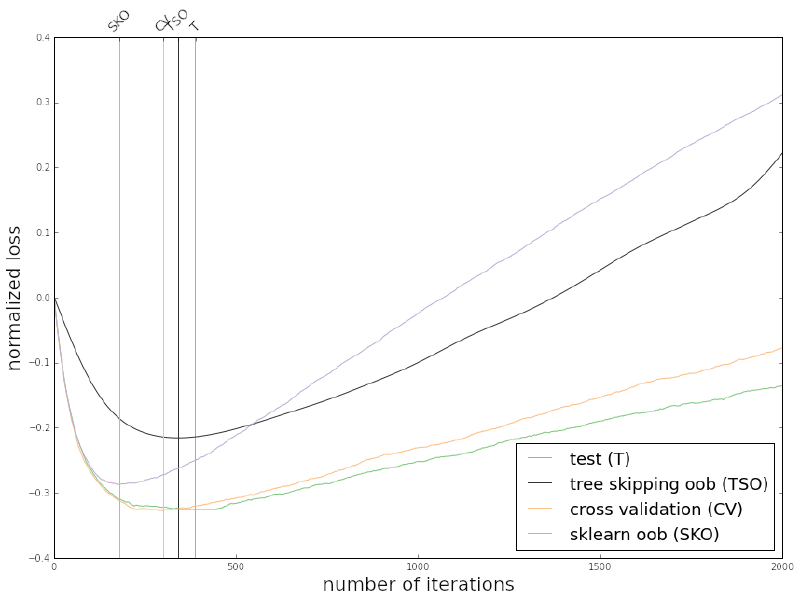
My approach (TSO) beat both 5-fold cross-validation (CV) and the GBM/scikit-learn method (SKO), as TSO obtains its minimum at the closest number of iterations to the test set’s (T) optimal value.
The next step in testing TSO’s viability was to rerun Ridgeway’s experiments from Section 3.3 of the GBM documentation (R code here). I used the same 12 UCI datasets that Ridgeway used, running 5×2 cross-validation on each one. For each dataset, the score was obtained by dividing the mean loss of the best method on the dataset by the loss of each method. Hence, all scores are between 0.0 and 1.0, with the best score being 1.0. The following figure summarises the results on the 12 datasets.
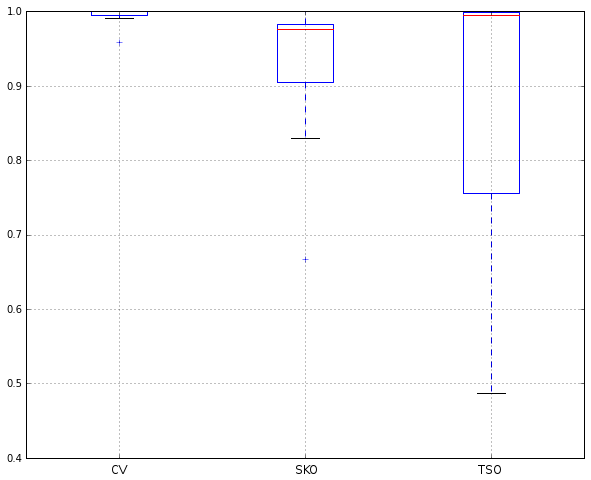
The following table shows the raw data that was used to produce the figure.
| Dataset | CV | SKO | TSO |
|---|---|---|---|
| creditrating | 0.9962 | 0.9771 | 1 |
| breastcancer | 1 | 0.6675 | 0.4869 |
| mushrooms | 0.9588 | 0.9963 | 1 |
| abalone | 1 | 0.9754 | 0.9963 |
| ionosphere | 0.9919 | 1 | 0.8129 |
| diabetes | 1 | 0.9869 | 0.9985 |
| autoprices | 1 | 0.9565 | 0.5839 |
| autompg | 1 | 0.8753 | 0.9948 |
| bostonhousing | 1 | 0.8299 | 0.5412 |
| haberman | 1 | 0.9793 | 0.9266 |
| cpuperformance | 0.9934 | 0.9160 | 1 |
| adult | 1 | 0.9824 | 0.9991 |
The main finding is that CV remains the most reliable approach. Even when CV is not the best-performing method, it’s not much worse than the best method (this is in line with Ridgeway’s findings). TSO yielded the best results on 3/12 of the datasets, and beat SKO 7/12 times. However, TSO’s results are the most variant of the three methods: when it fails, it often yields very poor results.
In conclusion, stick to cross-validation for the best results. It’s more computationally intensive than SKO and TSO, but can be parallelised. I still think that there may be a way to avoid cross-validation, perhaps by extending SKO/TSO in more intelligent ways (see some interesting ideas by Eugene Dubossarsky here and here). Any comments/ideas are very welcome.
Public comments are closed, but I love hearing from readers. Feel free to contact me with your thoughts.