Bootstrapping the right way?

Bootstrapping the right way is a talk I gave earlier this year at the YOW! Data conference in Sydney. You can now watch the video of the talk and have a look through the slides. The content of the talk is similar to a post I published on bootstrapping pitfalls, with some additional simulations.

The main takeaways shared in the talk are:

• Don’t compare single-sample confidence intervals by eye
• Use enough resamples (15K?)
• Use a solid bootstrapping package (e.g., Python ARCH)
• Use the right bootstrap for the job
• Consider going parametric Bayesian
• Test all the things

Testing all the things typically requires writing code, which I did for the talk. You can browse through it in this notebook. The most interesting findings from my tests are summarised by the following figure.

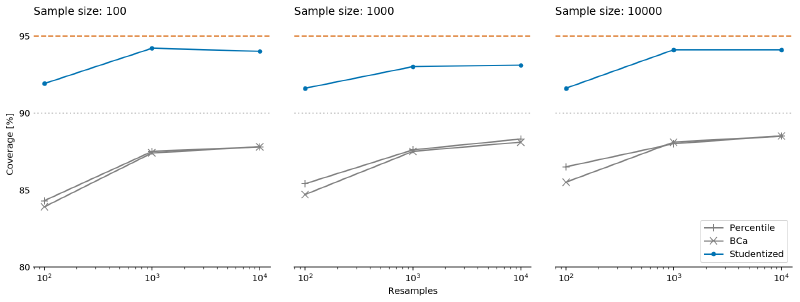
The figure shows how the accuracy of confidence interval estimation varies by algorithm, sample size, and the number of bootstrapping resamples on a synthetic revenue dataset. This sort of dataset may occur in freemium scenarios, where several product variations are offered at a few price tiers, including a price of zero (i.e., free). In all cases, the dashed line denotes the requested confidence level of 95%, i.e., the true difference in means between the two revenue distributions should be inside the confidence interval in approximately 95% of the simulations for it to be accurate. Unfortunately, it is clear that both the percentile and BCa algorithms perform poorly on the simulated data. Even with a sample size of 10K, they both yield “95%” confidence intervals that contain the true difference in means less than 90% of the time, i.e., the intervals are too narrow. By contrast, the studentized algorithm gets much closer to the requested confidence level, but this comes at the price of considerably longer runtime due to the need for nested bootstrapping.

Note that the results presented in the talk are slightly different from the figure above. The difference is due to a small bug in the simulation code: I used a constant random seed for all the bootstrapping simulation iterations (every iteration still contained different data). This has led to the surprising finding that accuracy with 10,000 resamples was lower than with 1,000 resamples. I attributed that finding to dataset quirks, and noted that my results may not generalise to all cases. Indeed, I recently ran a similar set of experiments on different data as part of my work at Automattic, and found that the studentized algorithm accuracy wasn’t as impressive as the results shown here.

In addition to synthetic data, the experiments I ran at Automattic included an implementation of an idea by my colleague, Demet Dagdelen: Test accuracy on samples from the full population for a given period (e.g., all sales over a calendar year). In such cases, the full population is well-defined. Therefore, we know the value of the “true” parameters, and we can run the same simulations as on synthetic data. While I can’t share that data, I can say that all algorithms performed much worse on real data than on simulated data. Therefore, we decided to follow the penultimate takeaway and use a parametric Bayesian approach for modelling our data. We may share insights from that line of work on data.blog in the future. In the meantime, comments are very welcome!

Update: You can find more accurate simulations in this post.